烂尾了,暂时没时间继续学了,以后有机会补
前言
这里是课程笔记。
这是一门好课,深入浅出。
这门课不需要知道太多数学原理。Coursera上有习题,哔哩哔哩上字幕清晰。
第1周
Welcome
- 机器学习是一门让计算机无需显式编程
(explicitly programmed)就能自主学习的学科。 - 计算机程序从经验
E中学习解决某一任务T,进行某一性能度量P,通过P测定在T上的表现因经验E而提高。 - 监督学习和无监督学习是最主要的两类机器学习方法。
Introduction
- 监督学习:训练数据有标签
- 回归问题:连续值预测
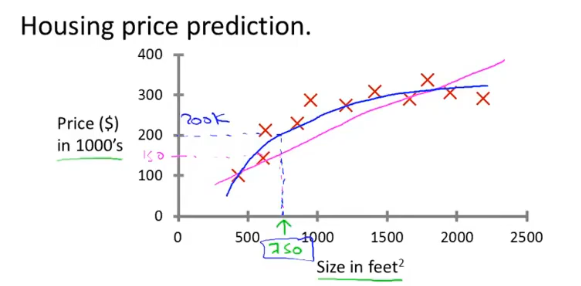
- 分类问题:离散值预测
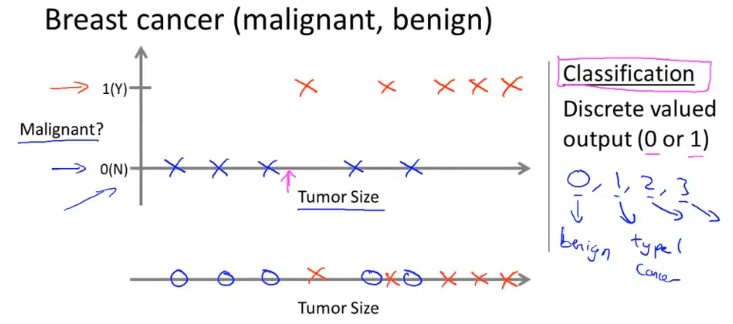
- 回归问题:连续值预测
- 无监督学习:训练数据无标签
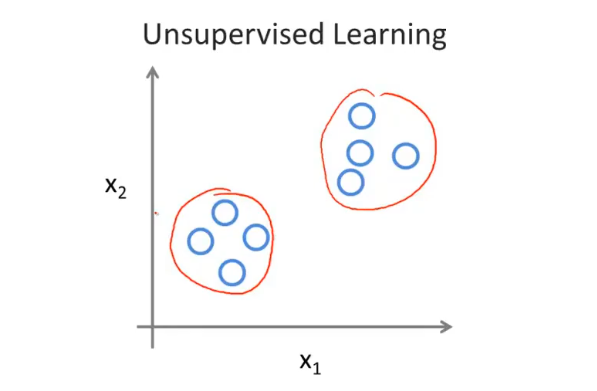
Model and Cost Function
符号定义
m:训练样本的数量x:输入变量y:输出变量(x, y):一个训练样本- 上标
i:训练集的索引 h:假设函数α:学习率
模型描述
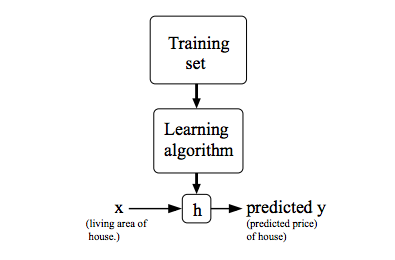

Parameter Learning

- 应当同步更新所有参数
- 若学习率过小,则需要很多步才能达到全局最低点
- 若学习率过大,则可能无法收敛或发散
- 若达到局部最低点,则参数值将不再变化(偏导数为
0) - 尽管学习率保持不变,但随着梯度下降法的运行,偏导数不断减小,参数更新幅度也越来越小,最终收敛
- 对于线性回归,总是会收敛到全局最优处
- 这也被称作
batch梯度下降法,即每一步梯度下降都遍历整个训练集的样本
第2周
Multivariate Linear Regression
符号定义
n:特征量的数目- 下标
j:特征的索引 X:设计矩阵
模型描述
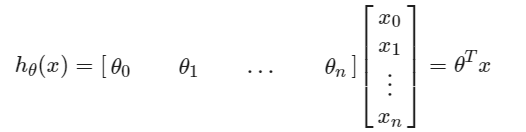

梯度下降

特征缩放
- 使不同特征的取值在相近的范围内,这样梯度下降法就能更快地收敛
- 我们通常将特征的取值约束到
-1到+1的范围内 - 归一化
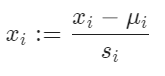
学习率
- 画出代价函数随迭代步数增加的变化曲线来判断梯度下降法是否已经收敛
- 若代价函数值不断增大,则梯度下降法没有正常工作,通常应该减小学习率
- 若代价函数图线上升再下降再上升再下降,通常也应该减小学习率
- 尝试不同的学习率:…,
0.001,0.003,0.01,0.03,0.1,0.3,1,…
特征与多项式回归
改造特征(乘方)形成多项式回归以更好地拟合曲线
Computing Parameters Analytically
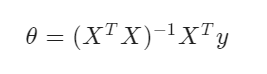
- 正规方程法避免了尝试不同学习率的麻烦
- 正规方程法适合相对不大的数据集(时间复杂度大约是
n的三次方)
向量化(important)
在写代码的时候很有用
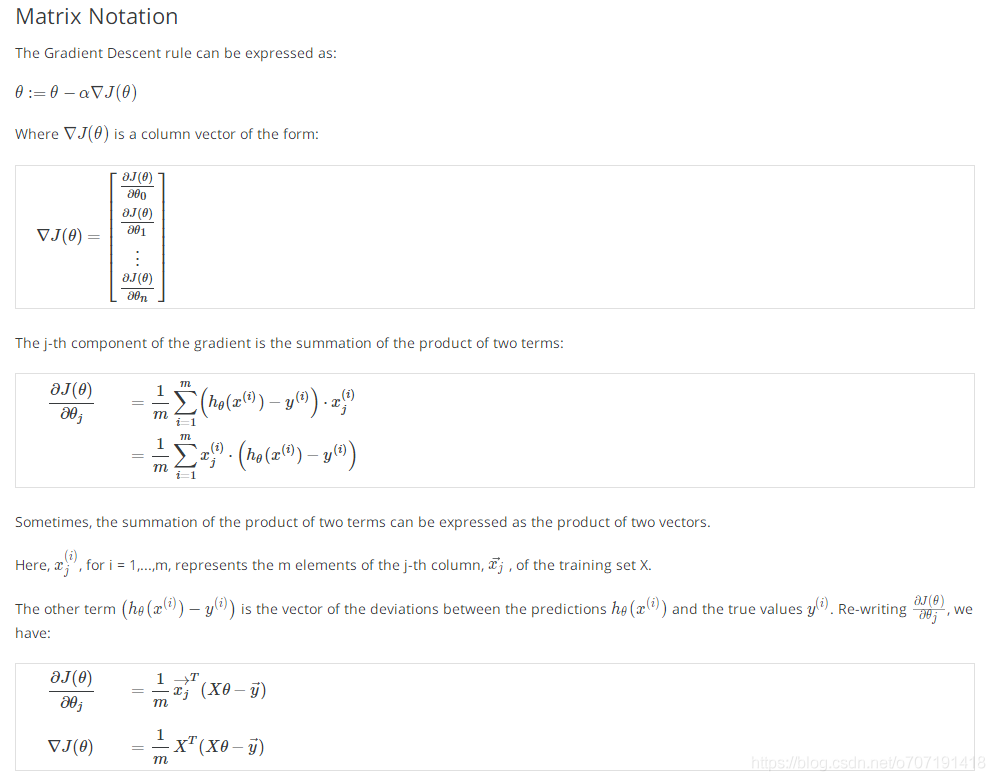

第3周
Classification and Representation
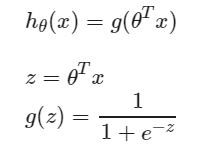
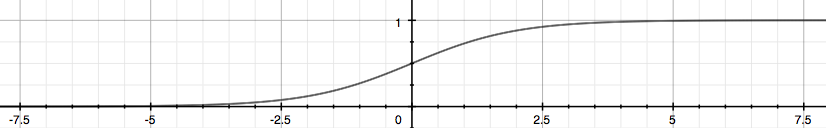
h(x):决策界限
Logistic Regression Model
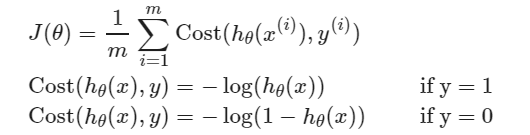
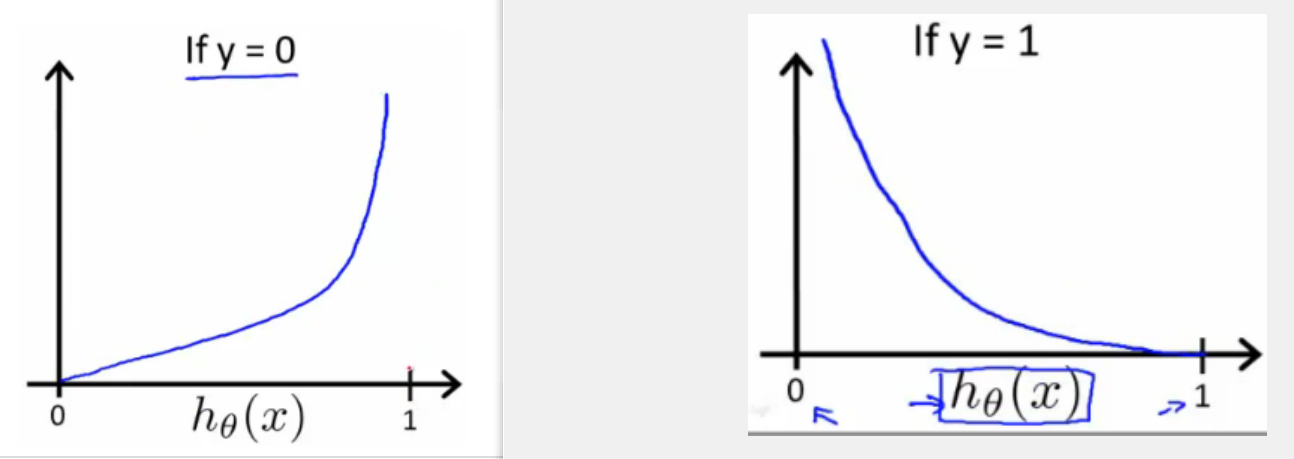

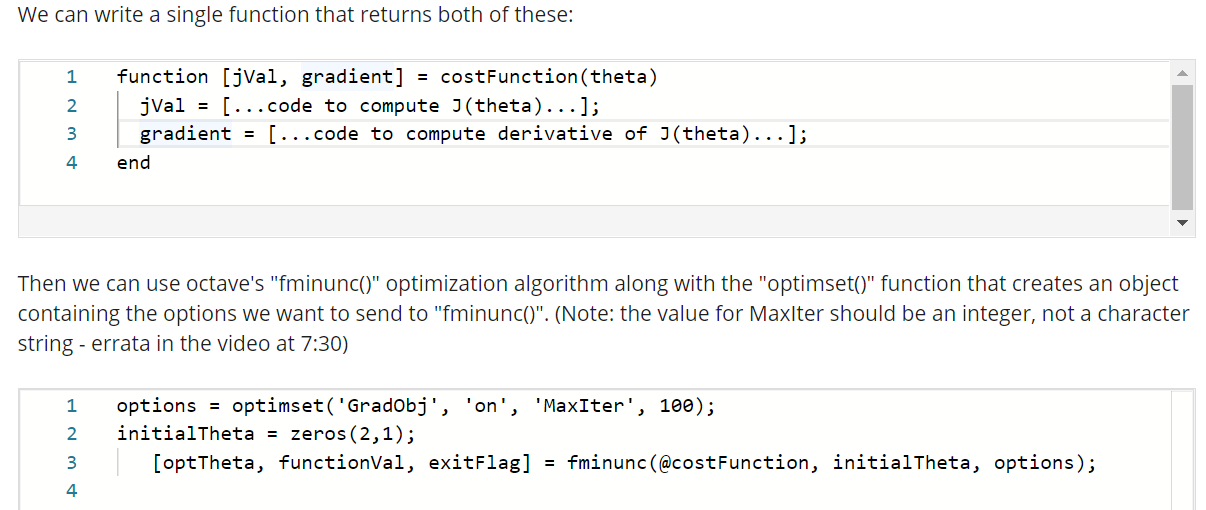
Multiclass Classification
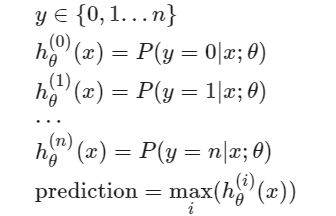
Solving the Problem of Overfitting
- 减少选取变量的数量
- 人工选择
- 模型选择
- 正则化
- 减小量级
- 众多变量都对预测值产生一定的影响
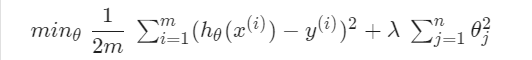
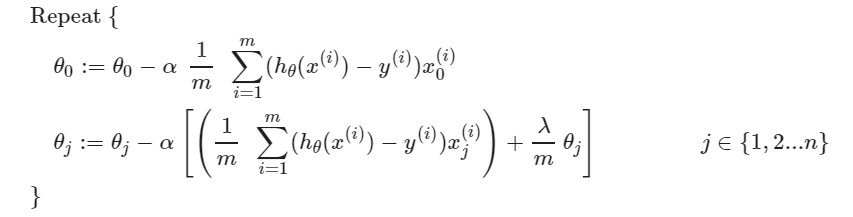
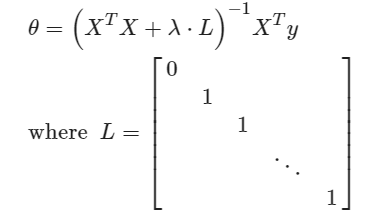
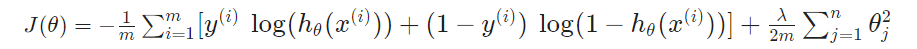
第3周
Motivations
Neural Networks






